K-meansクラスタリング
概要
- クラスタリングとは、データをいくつかのグループに分ける教師なし学習
- K-Meansはその中の1つで、クラスタ中心からの距離をもとにクラスターの分類を行う
流れ
- データセットの読み込み
- データの標準化
- クラスターの数を決定する
- クラスタリング
Google Colabでk-meansクラスタリング
必要なモジュール・パッケージをインポートします。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import preprocessing
from sklearn.cluster import KMeans
まずは、データの読み込みと表示を行い、どのようなデータなのかを確認します。 pandasのDataFrameというデータ構造で保持します。
df = pd.read_csv("/content/sample_data/california_housing_train.csv")
df.head()

データの読み込みと表示
簡単にデータの分布を見てみます。seabornなど可視化用のライブラリを用いた方が綺麗に表示できます。
df.hist(bins=50, figsize=(20, 15))
plt.show()
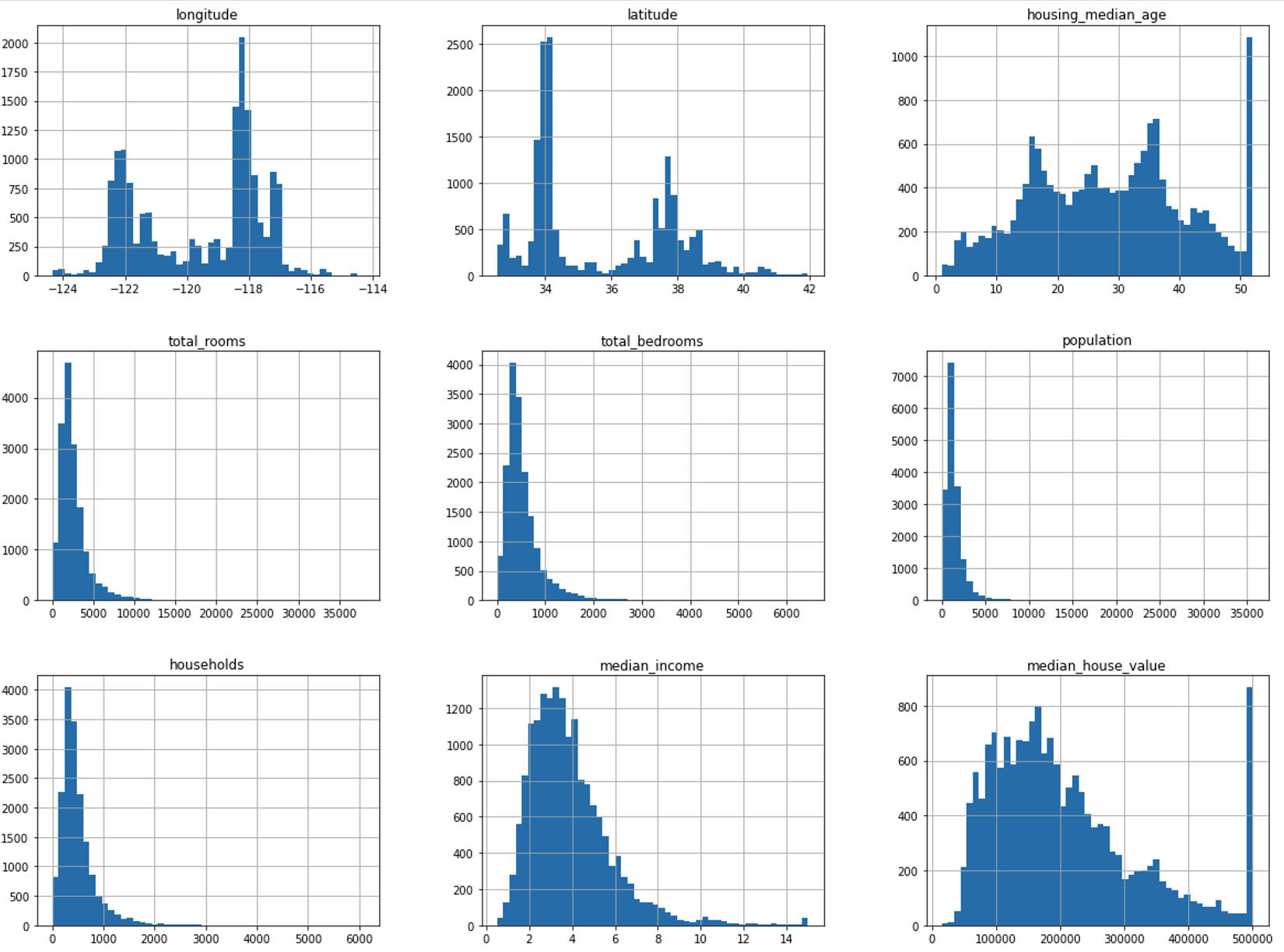
まずは、どういう分布のデータなのかを見る
次にデータの標準化を行い、各特徴量のスケールを合わせます。
X = df.copy()
sc = preprocessing.StandardScaler()
sc.fit(X)
X_norm = sc.transform(X)
クラスタリングをするための準備ができました。 k-meansクラスタリングは、いくつのクラスターに分類するかを前もって決めないといけない教師なし学習です。どれくらいのクラスター数が適当なのかをelbow法を用いて決めます。
start, end = 1, 30
dist_list = []
for i in range(start, end):
kmeans = KMeans(n_clusters=i, init='k-means++', random_state=7)
kmeans.fit(X_norm)
dist_list.append(kmeans.inertia_)
plt.plot(range(start, end), dist_list, marker='+')
plt.title('elbow method')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.show()
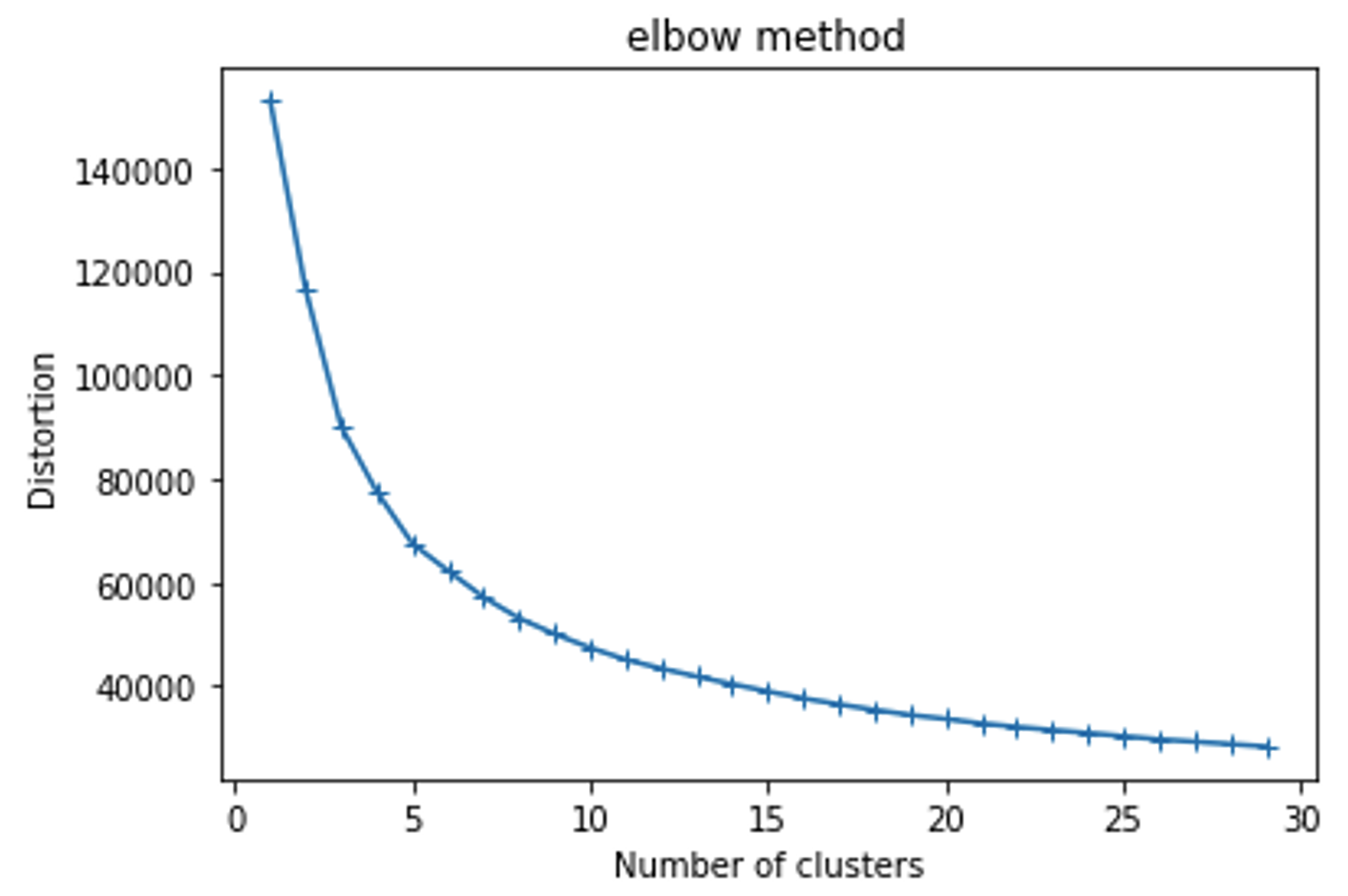
カクッと曲がり始めたところを目安にクラスター数を決める
次に、elbow法で決めたクラスター数をもとにクラスタリングを行います。
# kmeansモデルの作成
kmeans = KMeans(n_clusters=5, init='k-means++', random_state=7)
# クラスターの重心
result = kmeans.fit(X_norm)
得られた結果は元のデータフレームと結合させます。
# クラスター番号の予測
y_pred = kmeans.predict(X_norm)
# クラスター番号をpandasのSeriesで保持
labels = pd.Series(kmeans.labels_, name='cluster')
print(labels.value_counts(sort=False))
# 元データにクラスター番号の結合
df_merge = pd.concat([df, labels], axis=1)
clusterという列が追加されているか確認を行います。
df_merge.head()

一番右に追加されている
最後に、各クラスターはどういう特徴を持っているのかを確認します。
fig, axes = plt.subplots(3, 3, figsize=(20, 15))
cols = df_merge.columns
axes = axes.ravel()
for col, ax in zip(cols, axes):
ax.set_title(col)
sns.violinplot(data=df_merge, x="cluster", y=col, palette="pastel", ax=ax)
plt.show()
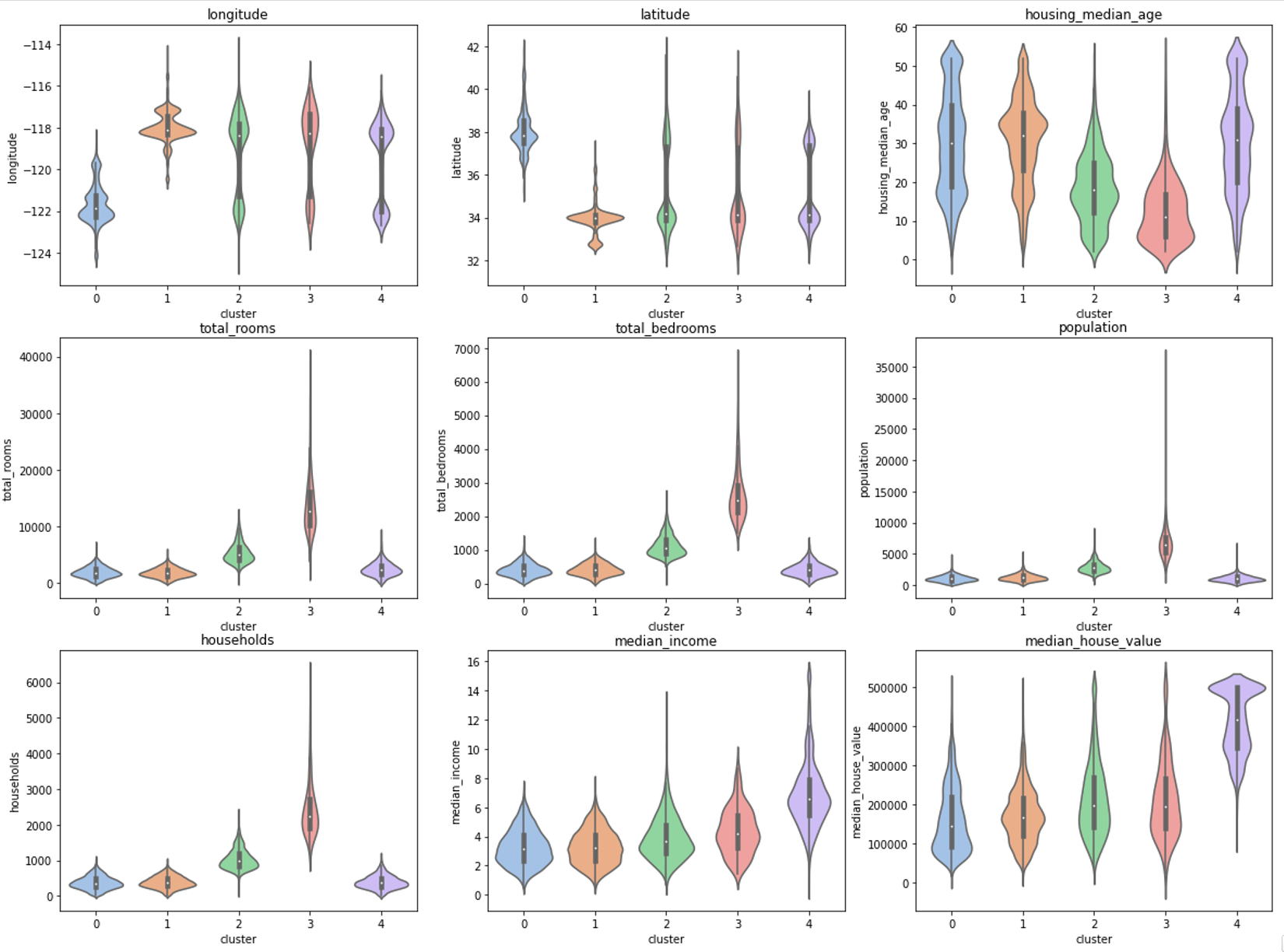
もし、標準化を行わなかった場合
座標空間上でデータ間の距離を用いているため、1つの特徴量のデータだけ絶対値が大きいとクラスタリングの結果に影響を与えてしまいます。
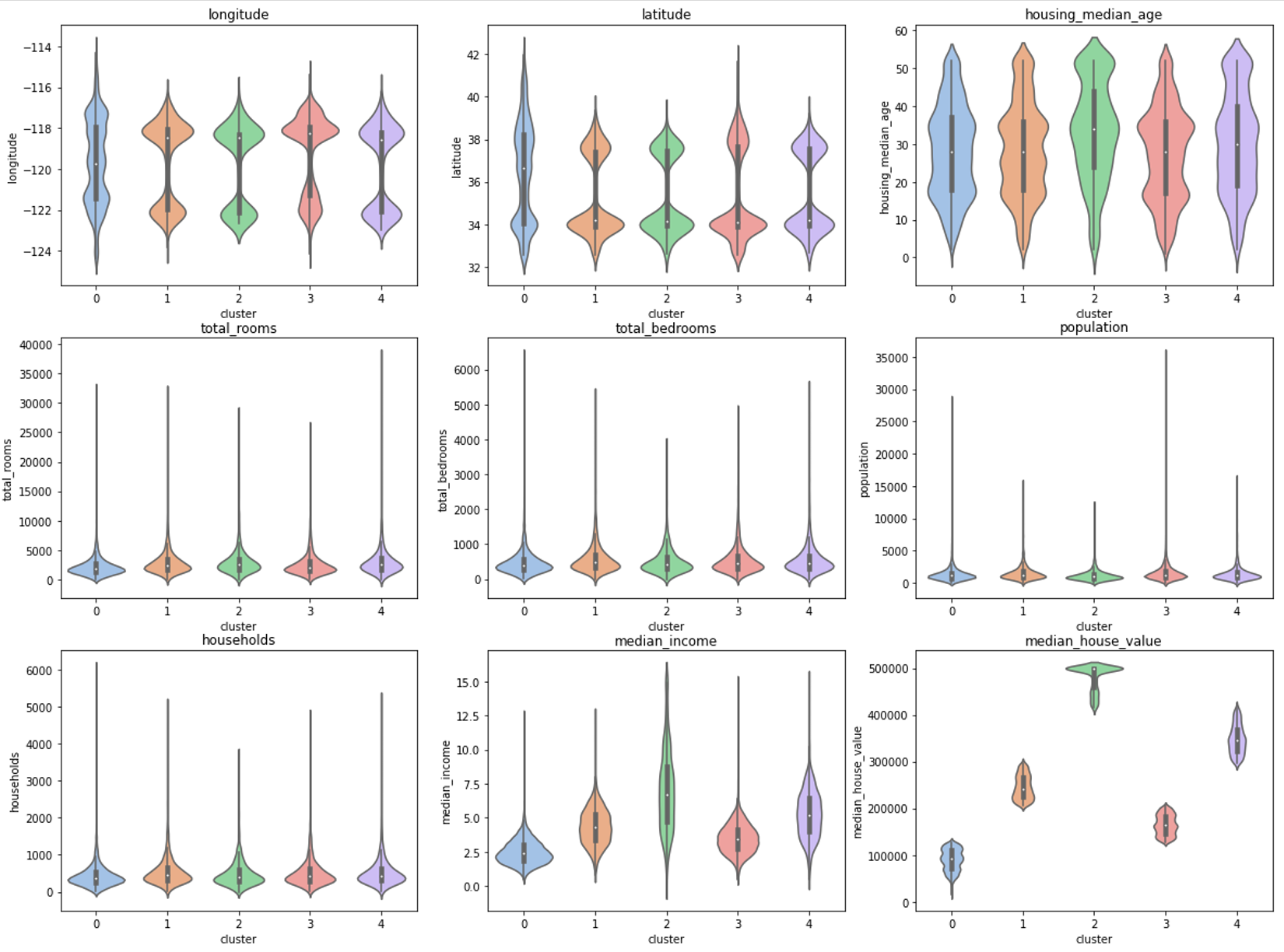
標準化を行わなかった場合
今回の場合、絶対値が最も大きかったmedian_house_valueという特徴量によってクラスターの分類がされていることが、上図からわかります。
median_incomeは絶対値が小さいのに影響しているように見えます。しかし、高価な家に住んでいる人の収入は高いことが予想されるため、median_incomeはmedian_house_valueの影響だと考えられます。